最近では、2次元だけではなく3次元画像の解析の必要性が高まってきています。
ここでは3次元画像解析を行うために必要な3次元画像構築、3次元画像解析の基礎を解説します。
3次元画像を構築することで実現できること
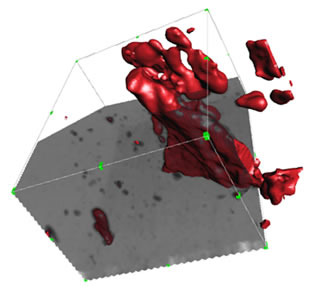
① 立体形状の可視化
円柱?球?断面では不明なZ軸方向の形状を可視化できます。
立体形状の可視化、これは2次元では円柱か球状が正確な形状は評価できないため、3次元を構築する必要があります。
② 表面形状の可視化
凹凸の有無、空隙の形状まで確認できます。
2次元画像でも対象物の変化は見れますが、凹凸や隙間の立体形状の評価には3次元での評価が必要です。
③ 断面観察
X-Y断面画像の3次元構築で、X-Z、Y-Zの断面を取得できます。
④ 3次元での定量化
3次元画像の構築だけでなく、対象物の体積、表面積等の測定ができます。
等値面の作成
3次元構築した画像は、2次元での解析と同様に、2値化して対象物を抽出します。
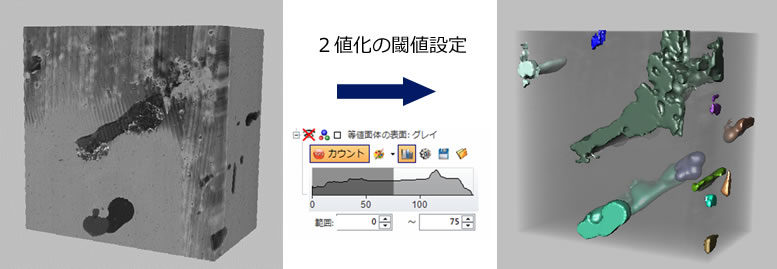
3次元構築での解析でも、2次元のフィルター処理のテクニック使用により、2値化を容易にすることができます。
連続断面画像の取得方法
3次元画像はX線CT、MRIだけでなく、連続断面画像を積層して3次元構築することもできます。
様々な方法がありますが、最近以下のような手法で高精度な連続断面が容易に取得可能になりました。
電子顕微鏡
FIB-SEM、SBF-SEM、TEMトモグラフィー、ATUM
光学顕微鏡
CT
MRI
3次元画像解析で測定できる形状
3次元測定では、任意の形状の測定が可能になります。
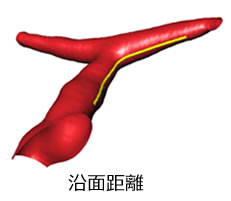
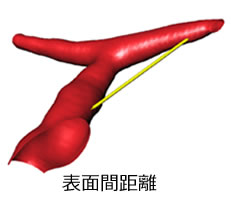
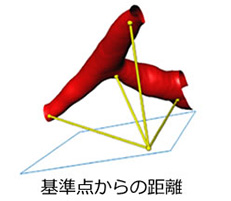
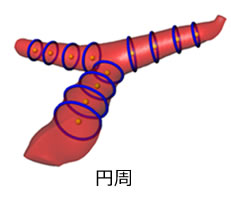
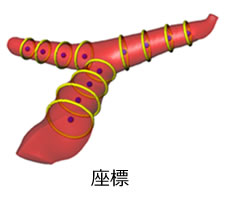
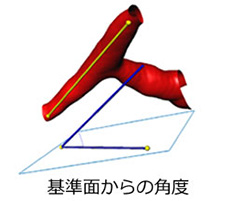
3次元対象物の抽出方法
長所:自由に描けるため、不鮮明な画像にも対応可能。
短所:作業者の知識、経験に依存するため、再現性に劣る。
連続画像では、多大な労力と時間を要する。
長所:属人性がなく、再現性が高い。
画像内の数値データに基づくため、科学的根拠がある。
自動処理であるため、人の労力、拘束時間を要しない。
短所:画像が2値化できない場合は、対応できない。

 HOME
HOME
